Penjelasan dan Rumus Barisan Geometri serta Contoh Soal Barisan Geometri

Selamat datang kembali sobat nara, setelah dua artikel terbaru saya membahas mengenai barisan aritmatika dan deret aritmatika, kali ini saya akan membahas kelanjutan dari dua artikel tersebut yaitu mengenai barisan geometri, bagi kalian yang belum mengerti mengenai barisan bilangan, kalian bisa membaca artikel sebelumnya karena masih akan berhubungan erat. Materi mengenai barisan geometri sebenarnya sudah diajarkan sejak bangku SMP dan kembali diulang di SMA, namun mengingat seringkali tes potensi akademik juga membahas barisan geometri maka saya ingin membahas bab ini.

Barisan Geometri

Barisan geometri adalah barisan yang memiliki perbandingan tetap pada tiap dua suku berurutannya, yang membedakan dengan barisan aritmatika adalah pada barisan aritmatika memilliki pertambahan atau pengurangan yang selalu tetap di tiap sukunya sedangkan pada barisan geometri, tiap suku yang berurutan memiliki perbandingan yang tetap bisa berupa perkalian atau pembagian. Untuk lebih jelasnya coba perhatikan contoh berikut

1. 2, 4, 8, 16, 32, …
2. 4, 16, 64, 256, …
3. 5, 25, 125, 625, …

jika kita perhatikan contoh di atas maka tiap tiap suku memiliki perbandingan yang tetap

a. 

b.

c.

dan perbandingan pada tiap suku berurutan ini dinamakan rasio dan dilambangkan dengan r

jadi pada barisan geometri akan terbentuk

U₁, U₂, U₃, U₄, U₅, U₆, U₇, …, U_n

a, ar, ar^², ar^³, ar^⁴, ar^⁵, ar^⁶, …, ar^^n-1

Jadi rumus untuk suku ke-n pada barisan geometri adalah

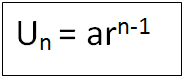
Keterangan :

U_n = suku ke-n

a = suku pertama

r = rasio

untuk mengecek pemahaman anda mengenai penjelasan di atas mari kita kerjakan contoh soal berikut

Contoh Soal

Contoh soal 1

Diketahui barisan geometri 5, 15, 45, 105, … Tentukan suku ke-15 dari barisan geometri tersebut

Jawab

a = 5

r = 15/5 = 3

Un = ar^^n-1

U₁₅ = 5 x 3^ ^15-1

U₁₅ = 5 x 3^ ¹⁴

U₁₅ = 5 x 4782969

U₁₅ =  23914845

Jadi suku ke-15 dari barisan tersebut adalah 23914845, tidak perlu kaget ya memang mengenai barisan geometri kalian akan menemui angka yang sangat besar atau sangat kecil

 

Contoh soal 2

Diketahui barisan geometri 6, 12, 24, 48, … Tentukan suku ke-10 dari barisan geometri tersebut

Jawab

a = 6

r = 12/6 = 2

Un = ar^^n-1

U₁₀ = 6 x 2^ ^10-1

U₁₀ = 6 x 2^ ⁹

U₁₀ = 6 x 512

U₁₀ =  3072

Jadi suku ke-10 dari barisan geometri tersebut adalah 3072

Contoh soal 3

Diketahui barisan geometri 4096, 1024, 256, 64, … Tentukan suku ke-8 dari barisan geometri tersebut

Jawab

a = 4096

r = 1024/4096 = 1/4

Un = ar^^n-1

U₈ = 4096 x (1/4)^ ^8-1

U₈ =4096 x (1/4)^ ⁷

U₈ = 4096 x 0,00006103515625

U₁₅ =  0,25

Jadi suku ke-8 dari barisan geometri tersebut adalah 0,25

Contoh soal 4

Suatu barisan geometri diketahui U₅ = 162 dan U₇ = 1458. Tentukan U₉ dari barisan tersebut

Jawab

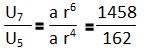
r^² = 9

r   = 3

Un = ar^^n-1

U₅ = a x 3^^5-1

162 = a x 3^⁴

162 = a x 81

a = 162/81

a = 2

Sehingga

Un = ar^^n-1

U₉ = a x 3^^9-1

U₉ = 2 x 3^⁸

U₉ = 2 x 6561

U₉ = 13122

Jadi suku ke-9 dari barisan geometri tersebut adalah 13122

Baca Juga : Penjelasan Rumus Barisan Aritmatika dan Contoh Soal Barisan Aritmatika
Baca Juga : Penjelasan Rumus Deret Aritmatika dan Contoh Soal Deret Aritmatika
Baca Juga : Penjelasan Rumus Deret Geometri dan Contoh Soal Deret Geometri

Contoh Soal 5

Suatu barisan geometri diketahui U₃ = 320 dan U₆ = 40. Tentukan U₈ dari barisan tersebut

Jawab

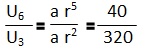
r^³ = 1/8

r   = 1/2

Un = ar^^n-1

U₃   = a x (1/2)^^3-1

320 = a x (1/2)^²

320 = a x 1/4

a = 320 x 4

a = 1280

Sehingga

Un = ar^^n-1

U₈ = a x (1/2)^^8-1

U₈ = 1280 x (1/2)^⁷

U₈ = 1280 x 1/128

U₈ = 10

Jadi suku ke-8 dari barisan geometri tersebut adalah 10

 

Contoh Soal 6

Tentukan rumus suku ke-n dari barisan geometri 64, 32, 16, 8, …

Jawab

r = U₂/U₁ = 32/64 = ½

Un = a x r^^n-1

Un = 64 x (1/2)^^n-1

Un = 64 x (2^^-1)^ ^n-1

Un = 2⁶ x (2)^ ^–n+1

Un = 2^^7-n

Jadi rumus suku ke-n dari barisan geometri di atas adalah Un = 2^^7-n