Penjelasan Rumus Deret Aritmatika dan Contoh Soal Deret Aritmatika dan Jawaban

Penjelasan Rumus Deret Aritmatika dan Contoh Soal Deret Aritmatika dan Jawaban – Kalau sebelumnya saya sudah membahas mengenai barisan aritmatika, kali ini saya akan membahas materi yang masih sangat erat hubungannya dengan barisan aritmatika yaitu deret aritmatika, perlu diketahui jika barisan dan deret itu berbeda. Untuk lebih memahami materi ini silahkan simak penjelasan mengenai deret di bawah ini.

Deret Bilangan

Deret bilangan adalah penjumlahan dari suku – suku barisan bilangan. Agar kalian tidak bingung perhatikan contoh berikut

Diketahui barisan bilangan sebagai berikut

1. 1, 3, 5, 7, 9, …
2. 5, 10, 15, 20, …
3. 2, 4, 8, 16, …
4. 48, 40, 32, 24, …

Deret bilangan dari barisan bilangan tersebut adalah

1. 1 + 3 + 5 + 7 + 9 + …
2. 5 + 10 + 15 + 20 + …
3. 2 + 4 + 8 + 16 + …
4. 48 + 40 + 32 + 24 + …

Saya yakin kalian semua sudah paham mengenai perbedaan barisan dan deret setelah memperhatikan contoh di atas.

Deret Aritmatika

Deret Aritmatika adalah jumlah dari seluruh suku – suku barisan aritmatika. Bentuk dari Deret Aritmatika adalah U₁ + U₂ + U₃ + U₄ + … + U_n dan dilambangkan dengan Sn

2 Sn = n (a + Un)

Sn = n/2 (a + Un)   ingat Un = a + (n-1)b

Sn = n/2 (a + a + (n-1)b)

Sn = n/2 (2a + (n-1)b)

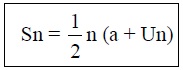
Keterangan :

Sn = Jumlah n suku deret aritmatika

Un = suku ke-n deret aritmatika

a   = suku pertama (U₁)

b   = beda

n   = banyakya suku

 

Berdasarkan rumus di atas kalian juga bisa mencari Un dengan memanfaatkan rumus Sn, yaitu

Un = S_n – S_n-1

Contoh Soal

Contoh 1

Sebuah deret aritmatika 4 + 9 + 14 + … , tentukan jumlah 20 suku pertama deret tersebut

Jawaban

B = U₂ – U₁ = 9 – 4 = 5

Sn = n/2 (2a + (n-1)b)

S₂₀ = 20/2 (2(4) + (20-1)5)

= 10 (8 + 95)

= 10(103)

= 1030

Jadi jumlah dari 20 suku pertama deret tersebut adalah 1030

Contoh 2

Suatu barisan aritmatika dengan suku ke-3 adalah 10 dan suku ke-9 adalah 28. Tentukan jumlah 16 suku pertama dari barisan tersebut

Jawaban

Untuk menjawab soal di atas kita harus mencari beda dan suku pertama dari barisan aritmatika tersebut

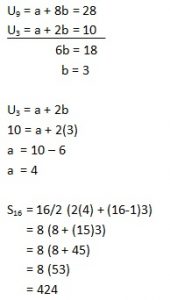
Jadi jumlah 15 suku pertama dari barisan aritmatika di atas adalah 424

Contoh 3

Suatu barisan aritmatika dengan suku ke-6 adalah 23 dan suku ke-12 adalah 47. Tentukan jumlah 30 suku pertama dari barisan tersebut

Jawaban

Untuk menjawab soal di atas kita harus mencari beda dan suku pertama dari barisan aritmatika tersebut

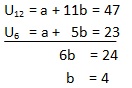
U₆ = a + 5b

23 = a + 5(4)

a  = 23 – 20

a  = 3

 

S₃₀ = 30/2 (2(3) + (30-1)4)

= 15 (6 + (29)4)

= 15 (6 + 116)

= 15 (122)

= 1830

Jadi jumlah 30 suku pertama dari barisan aritmatika di atas adalah 1830

Baca Juga : Penjelasan Rumus Rumus Barisan Aritmatika dan Contoh Soal Barisan Aritmatika
Baca Juga : Penjelasan Rumus Rumus Barisan Geometri dan Contoh Soal Barisan Geometri
Baca Juga : Penjelasan Rumus Rumus Deret Geometri dan Contoh Soal Deret Geometri

Contoh 4

Tentukan jumlah seluruh bilangan ganjil antara 50 dan 150

Jawaban

Untuk menjawab soal di atas kita harus membuat bentuk deret dari soal tersebut yaitu

51 + 53 + 55 + … + 149

Dari deret di atas kita sudah bisa mengetahui

a = 51

b = 2

Un = 149

Setelah itu kita cari nilai n

Un = (a + (n-1)b)

149 = (51 + (n-1)2)

149 = (51 +(2n – 2))

149 = 2n + 49

2n = 149 – 49

2n = 100

n = 50

Karena nilai n sudah ketemu langsung kita masukkan ke rumus Sn

Sn = n/2 (a + Un)

S₅₀= 50/2 (51 + 149)

= 25 (200)

= 5000

Jadi jumlah dari bilangan ganjil yang terletak di antara 50 sampai dengan 150 adalah 5000

Contoh 5

Suatu deret aritmatika dengan S₁₅ = 465 dan S₁₆ = 528. Tentukan U₁₆ dari barisan aritmatika tersebut

Jawaban

Un = S_n – S_n-1

U₁₆ = S₁₆ – S₁₅

       = 528 – 465

= 63

Jadi suku ke-16 dari barisan aritmatika di atas adalah 63