Penjelasan dan Rumus Deret Geometri serta Contoh Soal Deret geometri – Deret Geometri? Materi ini adalah kelanjutan dari artikel sebelumnya mengenai barisan geometri. Ya pada dasarnya hubungan antara deret geometri dengan barisan geometri adalah sama seperti hubungan deret aritmatika dengan barisan aritmatika, yaitu jumlah dari suku – suku pada barisan geometri adalah deret geometri, pembahasan mengenai deret bilangan juga telah saya bahas pada artikel sebelumnya, bagi kalian yang belum membaca silakan baca di sini. Mengingat perbedaan utama antara barisan aritmatika dan barisan geometri adalah pada barisan aritmatika tiap suku berurutan memiliki selisih yang sama sedangkan pada barisan geometri pada setiap suk berurutannya memiliki perbandingan yang sama.
Deret Geometri
Deret Geometri adalah jumlah suku – suku pada barisan geometri, jadi bentuk dari deret geomteri adalah U1 + U2 + U3 + U4 + U5 + … + Un dan dilambangkan sengan Sn, kalau kita hitungnya manual akan memakan waktu yang lama, jadi tidak perlu khawatir karena sudah ada rumusnya.
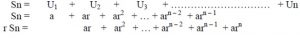
Sn – r Sn = a – arn
Sn (1 – r) = a (1 – rn) maka
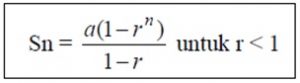
atau
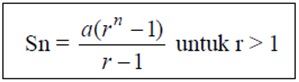
Keterangan :
Sn = Jumlah n suku pertama
a = suku pertama
r = rasio
n = banyaknya suku
Deret Geometri tak hingga
Deret geometri yang banyak suku – sukunya tak hingga disebut deret geometri tak hingga dengan bentuk umumnya a + ar + ar^2 + ar^3 + ar^4 + …
Deret geometri tak hingga hanya berlaku apabila nilai rasio adalah -1 < r < 1, jadi apabila di luar nilai tersebut maka tidak bisa disebut deret geometri tak hingga karena tidak memiliki limit jumlah
Untuk rumus deret geometri tak hingga adalah sebagai berikut
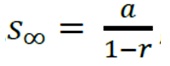
Dengan a adalah suku pertama dan r adalah rasio
Contoh :
Hitung limit jumlah dari deret geometri tak hingga
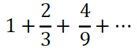
Jawab
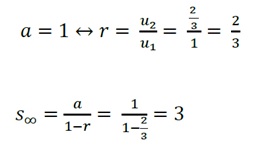
Untuk lebih memahami materi di atas coba perhatikan contoh soal berikut
Contoh Soal
Contoh Soal 1
Tentukan jumlah 10 suku pertama dari deret geometri 2 + 6 + 18 + …
Jawab
a = 2
r = U2/U1 = 6/2 = 3
Sn = a(r^n – 1)/r-1
S10 = 2(3^10 – 1)/ 3-1
S10 = 2(59049 – 1)/ 2
S10 = 2(59048)/ 2
S10 = 59048
Jadi jumlah 10 suku pertama dari deret geometri tersebut adalah 59048
Contoh soal 2
Tentukan jumlah 8 suku pertama dari deret geometri 640 + 320 + 160 + …
Jawab
a = 640
r = U2/U1 = 320/640 = ½
Sn = a(1 – r^n)/1 – r
S8 = 640(1 – (1/2)^8)/ 1 – ½
S8 = 640(1 – 0,003906)/ 0,5
S8 = 640(0,996094)/ 0,5
S8 = 637,5 / 0,5
S8 = 1275
Jadi jumlah 8 suku pertama dari deret geometri tersebut adalah 1275
Contoh Soal 3
Suatu deret geometri dengan suku pertama 3 dan rasio 3, Tentukan n jika Sn = 9840
Jawab
a = 3
r = 3
Sn = a(r^n – 1)/r-1
9840 = 3(3^n – 1)/ 3-1
9840 = 3(3^n – 1)/ 2
9840 x 2 = 3(3^n – 1)
19680 = 3(3^n – 1)
19680/3 = 3^n – 1
6560 = 3^n – 1
3^n = 6560 + 1
3^n = 6561
3^n = 3^8
n = 8
Jadi nilai n pada deret geometri tersebut adalah 8
Contoh soal 4
Suatu deret geometri dengan suku pertama 1440 dan rasio ½, Tentukan n jika Sn = 2790
Jawab
a = 1440
r = ½
Sn = a(1 – r^n )/1 – r
2790 = 1440(1 – (½ )^n)/ 1 – ½
2790 = 1440(1 – (½ )^n)/ ½
2790 x ½ = 1440(1 – (½ )^n)
1395 = 1440(1 – (½ )^n)
1395/1440 = 1 – (½ )^n
0,96875 = 1 – (½ )^n
(½ )^n = 1 -0,96875
(½ )^n = 0,03125
(½ )^n = (½ )5
n = 5
Jadi nilai n pada deret geometri tersebut adalah 5
Baca Juga : Penjelasan Rumus Barisan Aritmatika dan Contoh Soal Barisan Aritmatika
Baca Juga : Penjelasan Rumus Deret Aritmatika dan Contoh Soal Deret Aritmatika
Baca Juga : Penjelasan Rumus Barisan Geometri dan Contoh Soal Barisan Geometri






