Penjelasan Rumus Barisan Aritmatika dan Contoh Soal Barisan Aritmatika serta Jawaban

Penjelasan Rumus Barisan Aritmatika dan Contoh Soal Barisan Aritmatika serta Jawaban – Apa yang kalian pikirkan ketika mendengar kata barisan atau deret? Pasti kalian akan berpikir itu adalah sesuatu yang berjajar membentuk satu garis yang lurus, pemikiran kalian tentu tidak salah namun, barisan dan deret kali ini yang akan saya bahas adalah barisan dan deret dalam bidang ilmu Matematika lebih tepatnya mengenai barisan dan deret bilangan. Materi Barisan Aritmatika ini juga seringkali masuk Soal UN Matematika SMA semua jurusan, karena itu kalian harus benar benar memahami materi ini dan mengerjakan soalnya dengan cepat agar kalian diuntungkan dalam hal waktu. Buat kalian teman – teman yang butuh soal soal latihan, kalian dapat mengunjungi Edutore.com karena terdapat banyak soal semua mata pelajaran lengkap dan tentunya banyak diskon juga jika kalian mau berlangganan produk – produknya.

Sekarang kita kembali mengenai barisan aritmatika yang akan admin jelaskan, dan akan admin bahas dari dasar yaitu mengenai barisan bilangan. Pastikan kalian menyimak dengan baik agar kalian dapat nilai yang bagus di sekolah.

Barisan Bilangan

Barisan bilangan adalah susunan bilangan yang diurutkan dengan aturan tertentu atau pola tertentu, bentuk barisan bilangan adalah a₁, a_2, a_3, …, a_n.

Contoh :

1. 1, 3, 5, 7, 9, …
2. 5, 10, 15, 20, …
3. 2, 4, 8, 16, …
4. 48, 40, 32, 24, …
5. 2, 6, 8, 17, …
6. -4, 0, 5, -3, …

Pada contoh di atas bilangan – bilangan pada a, b, c, dan d adalah barisan karena urutan mereka memiliki aturan yang jelas entah itu ditambah, dikurangi, dikali, ataupun dibagi sedangakan bilangan – bilangan di e dan f bukan berupa barisan karena tidak adanya aturan yang menentukan urutan bilangan – bilangan tersebut.

Setiap bilangan yang berada pada barisan bilangan disebut dengan suku (U)

Suku pertama dilambangkan dengan a atau U₁

Suku kedua dilambangkan dengan U₂

Suku ketiga dilambangkan dengan U₃ sampai dengan suku ke-n (U_n)

Barisan Aritmatika

Barisan Aritmatika adalah barisan bilangan yang selisih antara tiap suku berurutan selalu tetap

Contoh :

1. 3, 6, 9, 12, 15, …

U₁ = 3, U₂ = 6, U₃ = 9, U₄ = 12, U₅ = 15

Selisih antara tiap suku berurutan :

U₅ – U₄ = 15 – 12 = 3

U₄ – U₃ = 12 – 9 = 3

U₃ – U₂ = 9 – 6 = 3

U₂ – U₁ = 6 – 3 = 3

Selisih antara tiap suku berurutan selalu sama yaitu 3

1. 3, 5, 7, 9, 11, …

U₁ = 3, U₂ = 5, U₃ = 7, U₄ = 9, U₅ = 11

Selisih antara tiap suku berurutan :

U₅ – U₄ = 11 – 9 = 2

U₄ – U₃ = 9 – 7 = 2

U₃ – U₂ = 7 – 5 = 2

U₂ – U₁ = 5 – 3 = 2

Selisih antara tiap suku berurutan selalu sama yaitu 2

Jadi, pada barisan aritmatika berlaku

U₂ – U₁ = U₃ – U₂ = … U_n – U_n-1 yang kemudian disebut dengan beda (selisih dua suku berurutan pada barisan aritmatika)

b = U_n – U_n-1

Jika suku pertama adalah a dan beda adalah b maka bentuk barisan aritmatika adalah seperti berikut

U1	U2	U3	…	Un
a	a+b	a+2b	…	a+(n-1)b

Jadi rumus untuk mencari suku ke-n barisan aritmatika adalah

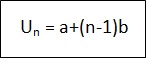
Untuk mencari suku tengah dari barisan aritmatika kalian bisa menggunakan rumus

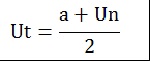
Contoh 1

Carilah 3 suku berikutnya dari barisan 7, 11, 15, 19, …

Jawaban :

a = 7

b = U₂ – U₁ = 11 – 7 = 4

U₅ = a+(5-1)b

U₅ = 7 + (4)4

U₅ = 7 + 16

U₅ = 23

U₆ = a+(6-1)b

U₆ = 7 + (5)4

U₆ = 7 + 20

U₆ = 27

U₇ = a+(7-1)b

U₇ = 7 + (6)4

U₇ = 7 + 24

U₇ = 31

Jadi 3 suku berikutnya dari barisan tersebut adalah 23, 27, 31

Contoh 2

Suatu barisan aritmatika diketahui suku ke 7 adalah 48 dan suku ke 11 adalah 76, tentukan suku ke-45

Jawaban :

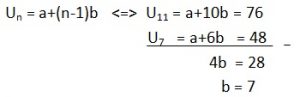
U₇   = a+6b

48   = a + 6(7)

48   = a + 42

a  = 48 – 42

a  = 6

 

U₄₅ = a+(n-1)b

U₄₅ = 6 + (45 – 1)7

U₄₅ = 6 + (44)7

U₄₅ = 6 + 308

U₄₅ = 314

Jadi suku ke-45 dari barisan aritmatika tersebut adalah 314

Contoh 3

Diketahui suatu barisan aritmatika dengan U₄ = 10 dan U₉ = 25. Tentukan suku ke-25

Jawaban

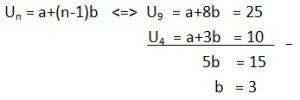
U₄   = a+3b

10   = a + 3(3)

10   = a + 9

a     = 10 – 9

a     = 1

 

U₂₅ = a+(n-1)b

U₂₅ = 1 + (25 – 1)3

U₂₅ = 1 + (24)3

U₂₅ = 1 + 72

U₂₅ = 73

Jadi suku ke-25 dari barisan aritmatika tersebut adalah 73

 

Contoh 4

Tentukan suku ke-9 dan rumus suku ke-n dari barisan aritmatika 7, 15, 23, 30, …

Jawaban

Untuk menjawab soal di atas kita harus mencari beda terlebih dahulu

b = U₂  – U₁

b = 15 – 7

b = 8

a = 7

U₉ = a + (8-1)b

U₉ = 7 + (7)8

U₉ = 7 + 56

U₉ = 63

Suku ke- 9 dari barisan aritmatika di atas adalah 63

U_n = a + (n-1)b

U_n = 7 + (n-1)8

U_n = 7 + (8n – 8)

U_n = 7 + 8n – 8

U_n = 8n – 1

Dan rumus suku ke-n untuk barisan aritmatika di atas adalah Un = 8n – 1

Baca Juga : Penjelasan Rumus Barisan Geometri dan Contoh Soal Barisan Geometri
Baca Juga : Penjelasan Rumus Deret Aritmatika dan Contoh Soal Deret Aritmatika
Baca Juga : Penjelasan Rumus Deret Geometri dan Contoh Soal Deret Geometri

Contoh 5

Sebuah  pabrik sepatu memproduksi 500 pasang sepatu pada awal tahun 2018, karena banyaknya permintaan sepatu di pasar, pabrik sepatu tersebut menambah produksi sepatu 25 pasang setiap bulannya. Berapa pasang jumlah sepatu yang diproduksi pabrik tersebut pada bulan terakhir tahun 2018?

Jawaban

Diketahui produksi pada awal tahun adalah 500 pasang maka a = 500 dan setiap bulan bertambah  25 maka b = 25

Yang ditanyakan produksi pada bulan desember (U₁₂)

U₁₂ = a + (n-1)b

U₁₂ = 500 + (12-1)25

U₁₂ = 500 + (11)25

U₁₂ = 500 + 275

U₁₂ = 775

Jadi produksi pada bulan Desember tahun 2018 sebanyak 775 pasang sepatu